Distribuições de Dados
Texto traduzido do Artigo: Overview of data distributions da Madalina Ciortan no Medium. Foram adicionados algumas informações ao texto e pretendo atualizá-lo com os exemplos das aplicações de cada distribuição.
Existem mais de 20 tipos diferentes de distribuição de dados (aplicados ao espaço contínuo ou discreto) comumente usadas na ciência de dados para modelar vários tipos de fenômenos.
Elas também têm muitas interconexões que nos permitem agrupá-los na família de distribuições.
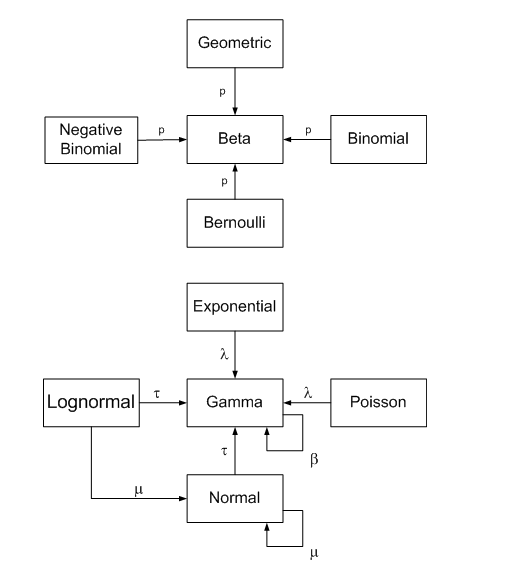
John D. Cook propõe em seu post a visualização abaixo, em que as linhas contínuas representam um relacionamento exato (caso especial, transformação ou soma) e a linha tracejada indica um relacionamento limite. O post também fornece uma explicação detalhada desses relacionamentos.

A seguir coloco informações sobre cada tipo de distribuição e quais fenômenos tipicamente modela, alguns exemplos de cenários que ilustram quando faz sentido escolher a distribuição, a distribuição de probabilidade / função de massa e sua forma típica em uma visualização.
A função densidade de probabilidade é uma aproximação contínua em termos de integrais da densidade de uma distribuição ou de uma versão suave de histogramas.
A função de distribuição cumulativa pode ser expressa como F (x) = P (X ≤x), indicando a probabilidade de X assumir um valor menor ou igual a x. As funções PMF se aplicam ao domínio discreto e fornecem a probabilidade de que uma variável aleatória discreta seja exatamente igual a algum valor.
Distribuições discretas
Uma distribuição discreta descreve a probabilidade de ocorrência de cada valor de uma variável aleatória discreta. Uma variável aleatória discreta é uma variável aleatória que tem valores contáveis, como uma lista de inteiros não negativos, como 1,2,3…
Distribuição de Bernoulli
A distribuição de Bernoulli é uma distribuição discreta que consiste em apenas um estudo com 2 resultados (sucesso / fracasso). Constitui a base para definir outras distribuições mais complexas, que analisam mais de uma tentativa, como as próximas 3 distribuições.

Distribuição binomial
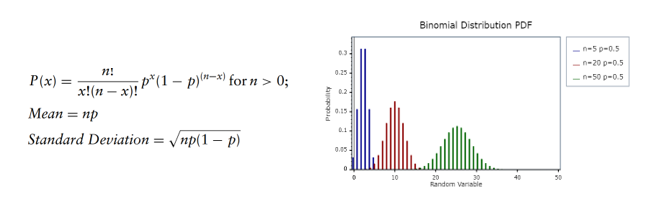
A distribuição binomial calcula a probabilidade de k sucessos em n tentativas. Como a distribuição de Bernoulli, os ensaios são independentes, ou seja um resultado não tem impacto no outro, e têm 2 resultados.
Exemplos de uso dessa distribuição são para estimar o número de caras dadas uma série de n lançamentos de moedas ou quantos bilhetes vencedores de loteria podemos esperar, considerando um número total de bilhetes comprados. Essa distribuição possui 2 parâmetros, no número total de tentativas e p a probabilidade de sucesso:
Distribuição Geométrica
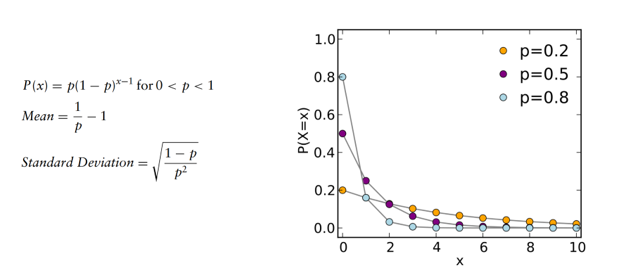
A distribuição geométrica calcula o número de tentativas antes que o primeiro sucesso ocorra. O número de tentativas não é fixo, a probabilidade de sucesso é a mesma nas tentativas independentes e a experiência continua até o primeiro sucesso. Essa distribuição possui um parâmetro, a probabilidade de sucesso p.
Por exemplo, suponha um dado que é atirado repetidamente até à primeira vez que aparece um “1”. A probabilidade de distribuição do número de vezes que o dado é atirado é suportado pelo conjunto infinito { 1, 2, 3, … } e é uma distribuição geométrica com a probabilidade p = 1/6.
Ou ainda imagine o exemplo onde nós podemos lançar uma moeda, repetidamente, até que seja observado uma “cara”, ou ainda, podemos lançar uma bola de basquete na cesta repetidamente até acertarmos.
Distribuição Hipergeométrica
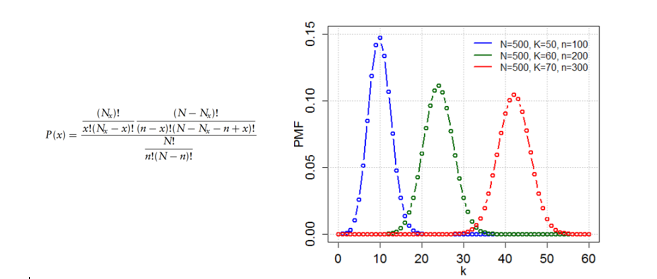
A distribuição hipergeométrica mede o número de sucessos em n tentativas (semelhante a binomial), mas não se baseia na suposição de independência entre as tentativas. Ou seja os testes são realizados sem substituição e cada teste altera a probabilidade de sucesso.
Exemplos são a probabilidade de retirar uma certa combinação de cartas de um baralho sem substituir ou de selecionar lâmpadas defeituosas de uma caixa com lâmpadas defeituosas e funcionando.
Essa distribuição depende do número de itens da população (N), do número de tentativas amostradas (n) e do número de itens da população com a característica de sucesso Nx. x representa o número de tentativas bem-sucedidas.
Distribuição Binomial Negativa
O binômio negativo calcula o número de tentativas até atingir r eventos de sucesso. É uma superdistribuição da distribuição geométrica e pode ser usada para modelar situações como o número de chamadas de vendas a serem realizadas para fechar r negócios.
Os parâmetros usados por esta distribuição são a probabilidade de sucesso p e o número de sucessos requeridos r.

Distribuição Uniforme Discreta
A Uniforme discreta é a distribuição de n resultados diferentes, mas igualmente prováveis. É a contrapartida da distribuição uniforme no espaço discreto. Toma como entrada apenas N, o número de resultados distintos.

Distribuição de Poisson
A distribuição de Poisson aproxima o número de vezes que um evento ocorre em um determinado intervalo, sabendo que as ocorrências são independentes, não há limite superior para o número de eventos e o número médio de ocorrências deve permanecer o mesmo se estendermos a análise intervalo para outro. Essa distribuição possui um parâmetro, sendo lambda o número médio de eventos por intervalo.

Distribuições contínuas
A distribuição contínua descreve as probabilidades dos possíveis valores de uma variável aleatória contínua. Uma variável aleatória contínua é uma variável aleatória com um conjunto de valores possíveis (conhecidos como a intervalos) que é infinito e incontável.
Distribuição beta
A distribuição beta é comumente usada para representar variabilidade em um intervalo fixo, por exemplo, para modelar o comportamento de variáveis aleatórias limitadas a intervalos de comprimento finito.
Também é uma opção adequada para modelar porcentagem ou proporções. Na inferência bayesiana, é usado para modelar o conjugado anterior para distribuições de Bernoulli, Binomial, Binomial negativo e geométrica.
Em termos mais simples, a distribuição beta é uma boa proposta para os anteriores (o conhecimento inicial de sucesso) para diferentes aplicações da família Bernoulli, como o número de coroas em testes de lançamento de moedas ou qualquer outro evento de resultado duplo.
São necessários 2 parâmetros, alfa e beta e a variável incerta é um valor aleatório entre 0 e um valor positivo. Diferentes combinações de alfa e beta levam às seguintes formas da distribuição:
- alpha == beta => distribuição simétrica
- se (alpha == 1 e beta> 1) ou (beta == 1 e alpha> 1) => distribuição em forma de J
- alfa < beta => inclinação positiva
- alfa > beta => inclinação negativa

Distribuição Dirichlet
A distribuição Dirichlet é uma generalização multivariada de distribuições beta, motivo pelo qual também é conhecida como distribuições Beta multivariadas.
É usada como distribuição prévia nas estatísticas bayesianas, onde é o conjugado anterior da distribuição categórica e multinomial.
É parametrizado por um vetor alfa de reais positivos e é amostrado em uma probabilidade simples. Um simplex de probabilidade é um conjunto de k números que somam 1 e que correspondem às probabilidades de k classes. Uma distribuição Dirichlet k-dimensional possui k parâmetros.
Distribuição Cauchy
A distribuição de Cauchy é empregada em teoria mecânica e elétrica, antropologia física e problemas de medição e calibração. Na física, descreve a distribuição da energia de um estado instável na mecânica quântica, sob o nome de distribuição Lorentziana.
Outra aplicação é modelar os pontos de impacto de uma linha reta fixa de partículas emitida a partir de uma fonte pontual ou em estudos de robustez. A distribuição de Cauchy é conhecida por ser uma distribuição patológica, pois sua média e variância são indefinidas. São necessários dois parâmetros. Nas estatísticas bayesianas, a distribuição de Cauchy pode ser usada para modelar os anteriores dos coeficientes de regressão na regressão logística.
A distribuição usa dois parâmetros, o modo m (correspondente ao pico) e a escala gama (meia largura na metade máxima da distribuição). A distribuição Cauchy é a distribuição T do aluno com 1 grau de liberdade.

Distribuição Qui-Quadrado
Essa distribuição é predominantemente usada no teste de hipóteses, na construção de intervalos de confiança, na avaliação da qualidade do ajuste de uma distribuição observada a uma distribuição teórica.
A variável qui-quadrado (com um grau de liberdade) é o quadrado de uma variável normal padrão e a distribuição de qui-quadrado possui propriedades aditivas (a soma de duas distribuições independentes de qui-quadrado também é uma variável de qui-quadrado).
A soma de k distribuições normais independentes é distribuída como um qui-quadrado com k graus de liberdade. A distribuição qui-quadrado também pode ser modelada usando uma distribuição gama com o parâmetro de forma como k / 2 e escala como 2S².
A distribuição qui-quadrado tem um parâmetro: k, o número de graus de liberdade.

Distribuição exponencial
Esta distribuição descreve a quantidade de tempo entre os eventos que ocorrem em momentos aleatórios. Considera-se que o tempo não afeta os resultados futuros (a vida útil futura de um objeto tem a mesma distribuição, independentemente do tempo em que ele existia), o que torna o exponencial “sem memória”. Ele pode ser usado para modelar situações como: quanto tempo temos que esperar em uma encruzilhada até vermos um carro rodando no sinal vermelho ou quanto tempo levará até que alguém receba a próxima ligação? quanto tempo um produto funcionará antes de quebrar?
A distribuição exponencial está relacionada a Poisson, que não descreve o tempo decorrido, mas o número de ocorrências de um evento em um determinado período. A distribuição exponencial é parametrizada apenas por lambda, a taxa de sucesso.

Distribuição de valor extremo (Gumbel)
A distribuição Gumbel modela a distribuição do máximo (ou mínimo) de um número de amostras de várias distribuições. Exemplos dessa distribuição são as forças de ruptura dos materiais, a carga máxima de uma aeronave, estudos de tolerância, o nível máximo de um rio ou de um terremoto em um determinado ano. Essa distribuição possui 2 parâmetros, o modo m corresponde ao ponto mais provável (ou o pico mais alto do PDF) e um parâmetro de escala, beta que é> 0 e controla a variação.

Distribuição F
Essa distribuição é usada para testar a diferença estatística entre duas variações como parte de uma análise ANOVA de sentido único ou a significância geral de um modelo de regressão com testes f. Freqüentemente, é a distribuição nula (a distribuição de probabilidade quando a hipótese nula é verdadeira) das estatísticas de teste. Toma como parâmetros n graus de liberdade para o numerador e m graus de liberdade para o denominador.

Distribuição Gama
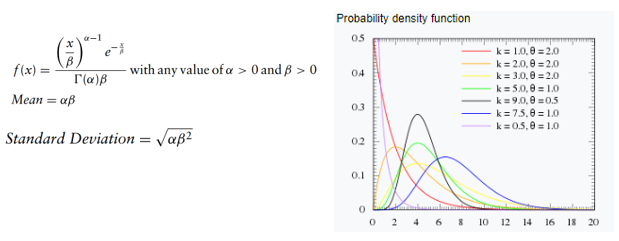
A distribuição gama é usada para medir o tempo entre a ocorrência de eventos quando o processo do evento não é completamente aleatório. O número de eventos no período estudado não se limita a um número fixo. Os eventos são independentes. A distribuição gama está relacionada às distribuições lognormal, exponencial de Pascal, Poisson e qui-quadrado. Pode ser usado para modelar concentrações de poluentes e quantidades de precipitação em processos meteorológicos. Depende de 2 parâmetros, alfa ou o parâmetro de forma e beta, o parâmetro de escala.
Um caso especial surge quando alfa é um número inteiro positivo; nesse caso, a distribuição (também conhecida como distribuição Erlang) pode ser usada para prever tempos de espera em sistemas de filas.
Distribuição Logística
Essa distribuição é usada para descrever o crescimento populacional ao longo do tempo ou reações químicas. Essa distribuição é simétrica e utiliza 2 parâmetros: a média ou o valor médio e a escala, controlando a variação.

Distribuição Lognormal
A distribuição lognormal é um bom candidato para modelar valores inclinados positivamente que são ≥0. Por exemplo, a distribuição normal não pode ser usada para modelar os preços das ações porque tem um lado negativo e os preços das ações não podem cair abaixo de zero, portanto a distribuição normal do log é um bom candidato. Assim, se uma variável aleatória X é log-normalmente distribuída, então Y = ln (X) tem uma distribuição normal. Da mesma forma, se Y tiver uma distribuição normal, a função exponencial de Y, X = exp (Y), terá uma distribuição log-normal. A distribuição lognormal é descrita por 2 parâmetros, a média e o desvio padrão.

Distribuição Pareto
A distribuição de Pareto é uma distribuição de probabilidade da lei de potência usada para modelar fenômenos empíricos, como a distribuição de riqueza, as flutuações do preço das ações, a ocorrência de recursos naturais. A distribuição de Pareto foi vulgarizada sob o nome de princípio de Pareto (ou a “regra 80–20”, o princípio de Matthew), afirmando que, por exemplo, 80% da riqueza de uma sociedade é detida por 20% de sua população. No entanto, a distribuição de Pareto somente produz esse resultado para um valor de potência específico do parâmetro de entrada alfa (α = log45 ≈ 1,16). Em termos de parâmetros, essa distribuição depende da localização (o limite inferior da variável) e da forma que controla a variação.

Distribuição t de Student
Essa distribuição é normalmente usada para testar a significância estatística da diferença entre duas médias da amostra ou para estimar a média de uma população normalmente distribuída, ambas para amostras pequenas. A forma dessa distribuição se assemelha à forma de sino de um gaussiano leptocúrtico. O único parâmetro é o grau de liberdade r.

Distribuição Triangular
Esta distribuição descreve a situação em que os valores mínimo, máximo e mais provável de um evento são conhecidos. Os valores mínimo e máximo são fixos e o valor mais provável cai entre eles, formando uma distribuição em forma triangular. Por exemplo, essa distribuição pode descrever as vendas de um produto quando sabemos as estimativas mínimas, máximas e mais prováveis.

Distribuição Weibull
A distribuição de Weibull é fortemente empregada em testes de fadiga, p. descrever o tempo de falha em estudos de confiabilidade ou a resistência à ruptura de materiais em testes de controle de qualidade. Também pode ser usado para modelar quantidades físicas, como velocidade do vento. Depende de 3 parâmetros de entrada: a localização L, a forma alfa e a escala beta. Quando o parâmetro de forma = 1, ele se torna a distribuição exponencial.

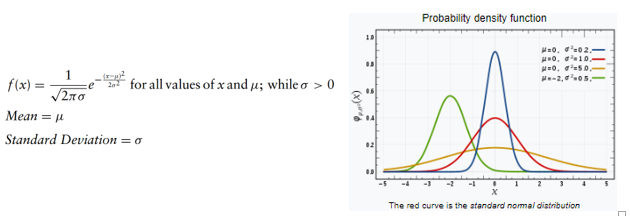
Distribuição normal
Provavelmente a distribuição mais estudada, a normal é usada para descrever fenômenos naturais, como a distribuição de alturas e escores de QI. Essa distribuição leva como entrada 2 parâmetros, a média e o desvio padrão.
Distribuições conjugadas
No contexto da análise bayesiana, se a distribuição posterior p (teta | x) e p (teta) anterior fazem parte da mesma família de probabilidades, elas são chamadas de distribuições conjugadas. Além disso, o prior chamou o conjugado prior para a função de verossimilhança.

Diferentes escolhas de prior podem tornar a integral mais ou menos difícil de calcular. Se a probabilidade p (x | teta) tiver a mesma forma algébrica que a anterior, podemos obter uma expressão de forma fechada para a posterior. Este blog fornece uma boa visão geral das relações entre a escolha da distribuição anterior (beta / gama) e a distribuição posterior da amostra.
Referências
https://onlinelibrary.wiley.com/doi/pdf/10.1002/9781119197096.app03
https://medium.com/@ciortanmadalina/overview-of-data-distributions-87d95a5cbf0a
https://probabilityandstats.wordpress.com/tag/poisson-gamma-mixture/
